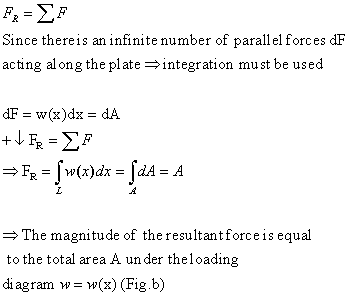Forces
and Moments: Part 8
Distributed
loading:
|
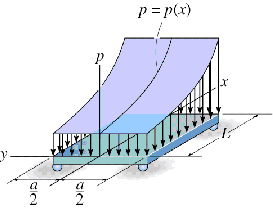
Wind, fluids, and the weight of a material supported over a body’s surface are examples of distributed loadings. Pressure p (force/unit area) is the intensity of these loadings. The loading
function is written as p=p(x) Pa or N/m2. Because
it is a function of [with the
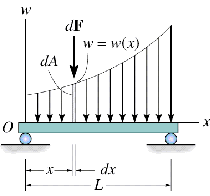
dimension of (N/m2)(m)=N/m] So w= w(x) N/m. The system of forces of intensity w=w(x) can be simplified into a single resultant force FR and its location x can be specified. Magnitude of the resultant force:
|
|
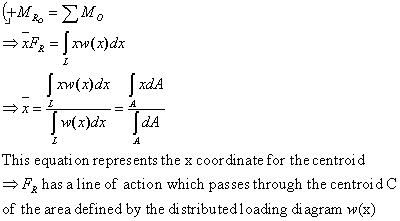
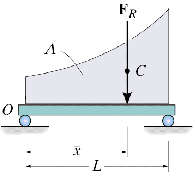
So in general, the magnitude of FR is defined by calculating the volume under the distributed loading curve p=p(x) and the location of resultant force is determined by finding the centroid of this volume.