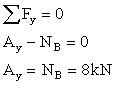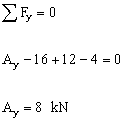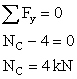Internal Forces:
Definitions:
The design of a structural member requires an investigation of the loading acting within the member to be sure the material can resist of carry the load.
As well as calculating the forces and moments transmitted through joints between members, we can also calculate the internal forces which one part of a member exerts on another. Internal loadings can be found by the method of sections.
To calculate these internal forces, simply:
- Draw a free-body diagram of the entire body,
- Find reactions at external supports,
- Find reactions at connections,
- Keep all loads in their exact locations,
- Pass a section cut through the member perpendicular to its axis at the point where the internal loads are to be determined,
- Draw FBD of cut member,
- For 2D problem find N, V, M (normal force, shear force and moment respectively) from equilibrium.
For example, consider the following member:
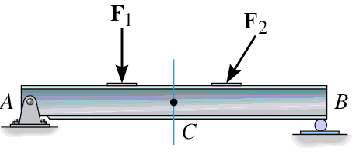
If you are interested in knowing the forces and moments that are transmitted through the member at point C; you can pass an imaginary section cut through C, cutting the beam into two segments:
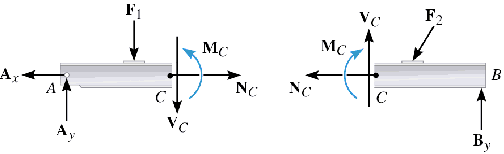
Note: The
forces and moment applied by the left-hand side onto the right-hand side are equal in
magnitude but opposite in direction to the forces applied by the right-hand side on the
left-hand side. Internal loadings on entire beam appear as external loads on the FBD of
the sections.
Each segment must be in equilibrium. We apply equilibrium equations to a segment and solve for internal force components.
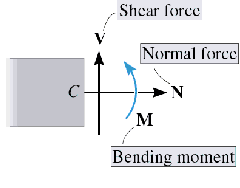
Two-dimensional beam
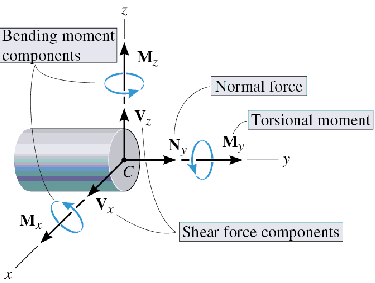
Three-dimensional beam
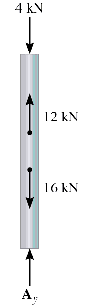
Example:
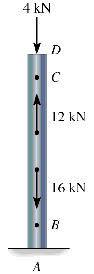
Determine the internal normal force at B and C and the reaction at A. |
|
Solution:
We start with the FBD of the entire bar and calculate the support reaction at A:
|
|
![]()