Equilibrium of rigid bodies: Part 4

Equilibrium in three dimensions:

 

Refer to ‘support reactions’ section and refresh your memory. Equilibrium equations are similar to those written in ‘Part 2’ of this section. We also have to consider the components in third dimension or z.

 

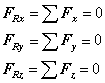
There are two methods for finding the unknown forces and moments:

 

Example:

 

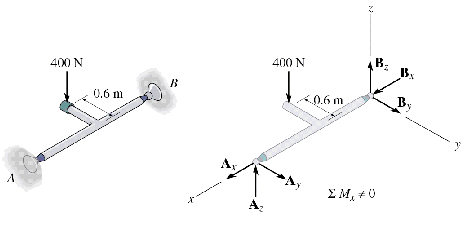
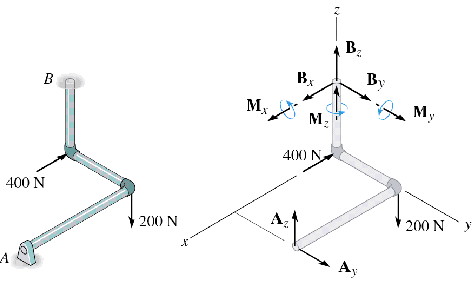
Draw the Free-body diagram of the shaft shown in the figure.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Solution:

 

1) Consider the plane passing from points A and B as the x-y plane,

2) Moment components are developed by the pin on the rod to prevent rotation about the x and z axes (no resistance from the pin against the rotation about the y axis:).

3) The string BC is a 2-force member which is under tension. Consider the tension T at the point B (force from the string).

 

 

In order to have a stable and proper system, the number of unknowns should be equal to that of equations. For instance, we have 6 unknowns for the example above and we also have 6 equations (three forces and three moments: )

Some constraints are either redundant or improper.

 

Improper constraints:

Number of equations could be equal to that of unknowns but the body could be instable because of improper constraining by supports.

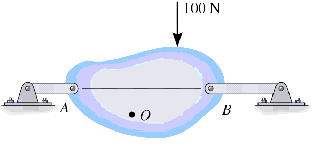
In 2D problems, the support reactions all intersect the same point, so the constraints are improper. Here, the 100N force causes a moment which is not restrained by any of the support constraints.

 

In 3D problems like this, the support reactions all intersect a common axis, so the constraints are improper. Constraints A and B are not proper, since they do not resist the moment caused by 400N force.

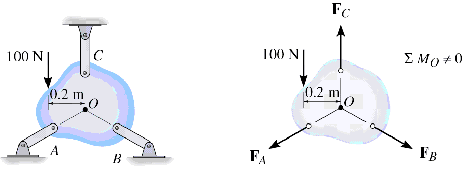
In the following figure, the reaction forces are all parallel, so the constraints are improper. The body will move under the exerted 100N force.

Redundant constraints:

Redundant supports are those more than necessary, under which the body becomes statically indeterminate. Also, unknowns are more than equations. The following figures are examples of redundant constraints.

When there are fewer reactive forces than the equations of equilibrium, they constraints are called Partially Constrained.