3. A ladder of weight 60 Nt leans against a frictionless wall. The other end of the ladder is on a floor where the coefficient of static friction is 0.3.
What is the maximum distance at which the bottom of the ladder in the problem above can be placed away from the wall before the ladder slips?
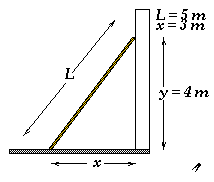
Solution:
All of our force diagrams will appear the same. The only things that have changed is that now x and y no longer equal 3 m and 4 m, respectively. However, it must still be true that (5 m)2 = x2 + y2. Also, we see that the frictional force does point to the right as we assumed in the force diagram for the previous problem, so the static frictional force will have to go to its maximum value, mus FN = (0.3)(60 Nt) = 18 Nt, to keep the ladder from slipping. From our x equation of motion, we have
max(Fw) = max( fs
) = 18 Nt
To get the maximum distance of the bottom of the ladder from
the wall, we use the torque equation from the previous problem to determine the maximum
value of q.
max(Fw) = � W cot (qmax) ==>
qmax = arccot[2max(Fw)/ W]
= arccot[2(18 Nt)/(60 Nt)] = 59�
This maximum value of q corresponds to a maximum distance
from the wall as follows:
L. sin(qmax) = xmax = (5 m)sin(59� ) = 4.3 m

