Dot product: The dot product of two vectors yields a scalar:
A . B = C
Magnitude:
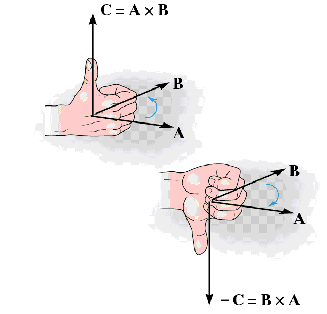
| Cross product: The cross product of two vectors yields a vector:
Magnitude: Direction:Vector C has a direction perpendicular to the plane containing A and B such that C is specified by the right hand rule. |
 |
| Laws of
operation:The Commutative Law is not valid:
|
 |
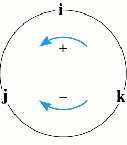
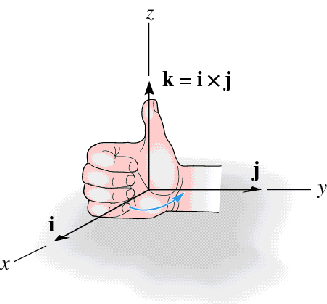
| Cross products of unit vectors: The direction is determined using the right hand rule. As shown in the diagram, for this case the direction is k and the Magnitude is: | i � j |=(1)(1)(sin90�) = (1)(1)(1)=1
so: i
� j = (1) k = k i � j = k
i � k = -j
i � i = 0 j � k = i
j � i = -k
j � j = 0 k � i = j k � j = -i k � k = 0
|
alphabetical order � + |
Cross product of two vectors in terms of their components:
A = Axi + Ayj +Azk
B = Bxi + Byj + Bzk
A � B = (Axi + Ayj +Azk) � (Bxi + Byj + Bzk)
+ AyBx (j � i) + AyBy (j � j) + AyBz (j � k)
+ AzBx (k � i) + AzBy (k � j) + AzBz (k � k)
= 0 + AxBy k – AxBz j - AyBx k + 0 + AyBz i + AzBx j – AzBy i + 0
Hence:
A � B = (AyBz – AzBy ) i - (AxBz -AzBx) j + (AxBy - AyBx ) k
This equation may also be written in a compact determinant form:
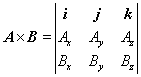
| For element i: | (i)(AyBz – AzBy
) |
 |
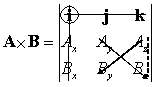| For element j: | (-j)(AxBz -AzBx) (notice the negative sign here) |
 |
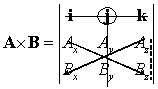| For element k: | (k)(AxBy - AyBx
) |
 |
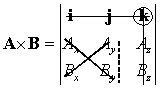Hence:
A � B = (AyBz
– AzBy ) i - (AxBz -AzBx)
j + (AxBy - AyBx
) k
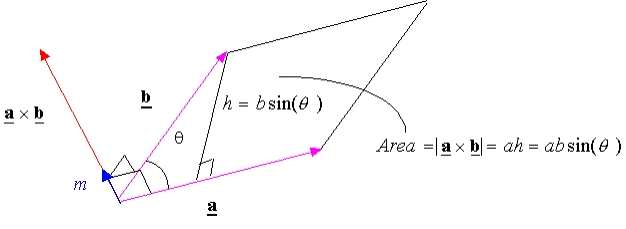
In summary, The cross product of vectors a and b is a vector perpendicular to both a and b and has a magnitude equal to area of the parallelogram generated from a and b. The direction of the cross product is given by the right hand rule (fingers from vector a to vector b and thumb is along vector c). Order is important in the cross product:
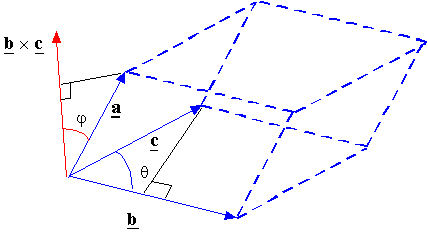
Triple product:
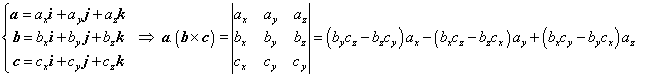
Back to Vectors
Next to Integral / Differentiation
