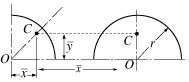Differentiation, Integration and Centroids
Differentiation (common
derivatives):
d/dx( c )= 0
The derivative of a constant is zero.
Example: d/dx 7 = 0
d/dx( c × x )= c
The rate of change of a linear function is its slope.
Example: d/dx 3 × x = 3
d/dx (xn) = n × x(n-1)
Example: d(x4)/dx = 4 × x 3
d/dx (log x) = 1/x
The derivative of the log of x is its inverse.
Example: d(log (x + 1))/dx = 1 / (x + 1)
d/dx (eax) = a eax
Example: d (e3x) /dx= 3 e3x
d/dx (sin cx) = c cos x
Example: d(sin3x) /dx = 3cos x
d/dx (cos x) = -sin x
Example: d (cos
![]() ) /dx= - sin
) /dx= - sin ![]()
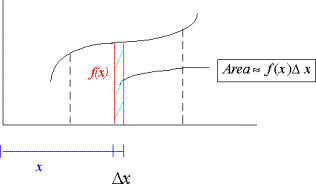
Integral of a function: The integral of a function f(x) over an interval from x1 to x2 yield the area under the curve in this interval

Note: The integral represents the![]() as
as ![]()
Some indefinite integrals to remember:
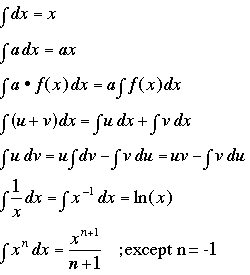

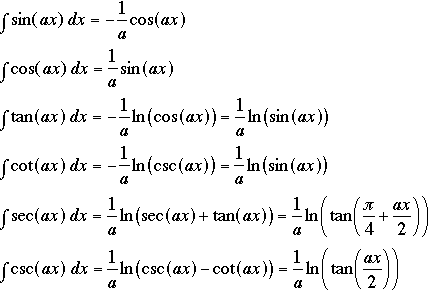
Note: Remember to add a constant of integration if you are not specifying limits. You evaluate the constant of integration by forcing the integral to pass through a known point.
Note: For definite integrals subtract the value of the integral at the lower limit from its value at the upper limit. For example, if you have the indefinite integral.
Note: The following notation is common
![]()
Integration by parts:
![]()
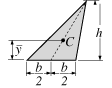
Centroid of an area:
The centroid of an area is the area weighted average location of the given area.
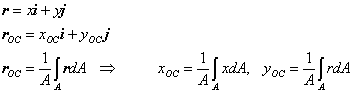
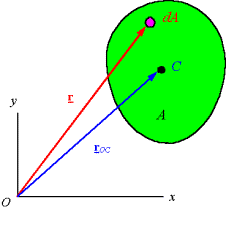
Centroids of common shapes:
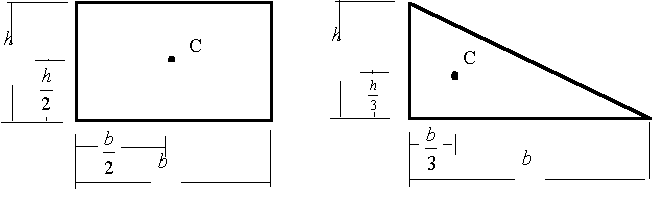
Some other centroids of common shapes of areas and lines are as follow:
Shapes |
Images |
|
|
Area |
Triangular Area |
|
|
|
|
|
||||
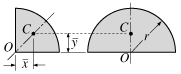
Quarter–circular area |
|
|
|
|
Semicircular area |
0 |
|
|
|
|
||||
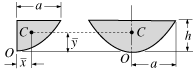
Semiparabolic area |
|
|
|
|
Parabolic area |
0 |
|
|
|
|
||||
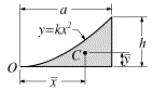
Parabolic spandrel |
|
|
|
|
|
||||
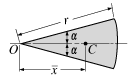
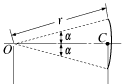
Circular Sector |
|
|
0 |
|
|
||||
Quarter-circular arc |
|
|
|
|
Semicircular arc |
0 |
|
|
|
|
||||
Arc of circle |
|
|
0 |
|
![]() Back to
Products
Back to
Products ![]() Next to Physics
Next to Physics